Boolean Algebra
Due: 11:00pm, Thursday October 29, 2020
Max grace days: 2
Problems
Problem 1
Find the output of the following circuit:
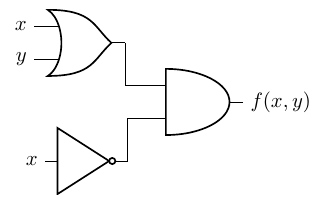
Problem 2
Find the output of the following circuit:
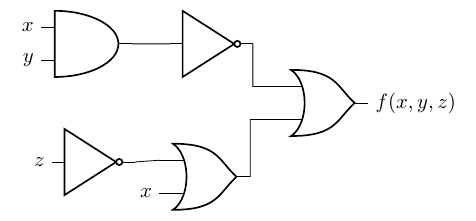
Problem 3
Draw a circuit for the function f(x,y,z) = x ⋅ y + x ⋅ z + y ⋅ z
Problem 4
Rewrite a + b using only NOT and two-input NAND.
Problem 5
Determine the input conditions for the following circuit so that f(a,b,c) = 1
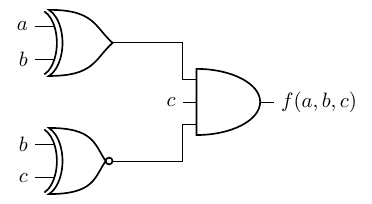
Problem 6
Show that $$\overline{a} \cdot \overline{c} + a \cdot \overline{c} + b \cdot c = b + \overline{c}$$
Problem 7
Simplify $$f(a, b, c) = a \cdot b + a \cdot c + c + \overline{a} \cdot b \cdot \overline{c}$$
Problem 8
Use a Karnaugh map to reduce $$f(a, b, c, d) = \overline{a} \cdot \overline{b} + a \cdot \overline{b} + \overline{c} \cdot \overline{d} + c \cdot \overline{d}$$ to a minimum sum of products form.
Problem 9
Design a circuit that takes a 4-bit binary number and produces 1 if the number is greater than twelve or less than three. Show the truth table, logic minimization and circuit diagram.
Problem 10
Design a circuit that takes a digit encoded as a 4-bit binary number and produces 1 if the number is greater than or equal to five. Show the truth table, Karnaugh map and circuit diagram. Note the Karnaugh map will have don’t care conditions for non-digit values.
Turning in the Assignment
Submit a single file containing your answers to the problems to the appropriate folder on D2L.
Grading Criteria
10 points per problem